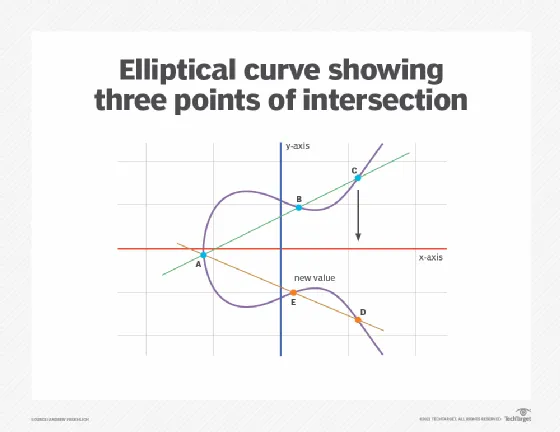
Elliptic-curve cryptography (ECC) is a type of public-key cryptography that is based on the algebraic structure of elliptic curves over finite fields. It is an alternative to traditional public-key cryptography algorithms such as RSA and is used for encryption, authentication, and digital signatures.
ECC generates keys through the properties of an elliptic curve equation instead of the traditional method of generation as the product of large prime numbers. The primary benefit of ECC over other public-key cryptography algorithms is that it allows for smaller key sizes while providing equivalent security. For example, a 256-bit elliptic curve public key should provide comparable security to a 3072-bit RSA public key. ECC is used in various real-world applications such as cryptocurrencies, digital signatures, and one-way encryption of emails, data, and software The U.S. government requires the use of ECC with a key size of either 256 or 384 bits for internal communications, depending on the sensitivity level of the information.